Categorical equality

One thing we tend to be very concerned with is whether things are the same. This is usually trivial to define when we have access to the underlying structure of objects: if two objects are such that their structures match up exactly, then we’ll say they’re equal and call it a day.

In category theory though, we don’t have access to this information. We need to define equality strictly through morphisms and their properties.

Let’s try to build an intuition of how we could express the fact that two objects, $A$ and $B$, are the same. Since we can only define this through the way they relate to other objects, we need to introduce a third one, $C$, for $A$ and $B$ to have relations with. Importantly, there’s nothing special about $C$: our reasoning must hold for any object.

Let’s take this step by step. Imagine that $C$ has a relation with $A$ - or, more formally, that there exists $s: C \to A$.

If $A$ and $B$ are the same, then we want $C$ to also have a relation with $B$; we want $t: C \to B$ to exist. And to ensure that this is always the case, we can use one of the properties of morphisms: composition. If we were to declare that, in order for $A$ and $B$ to be the same, there must exists $f: A \to B$, then we know that the $t$ we’re looking for will always exist: $t=f \circ s$.

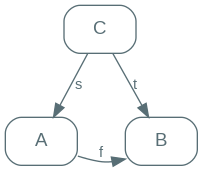
But $t$ cannot be just any morphism: if $A$ and $B$ are the same as far as $C$ is concerned, then whatever relation it has with $A$, it must have the same with $B$.

This notion - two morphisms being the same even though they do not connect the same objects - is something that I struggle with a little bit, but I like to think of it that way. If $s$ can be defined by using $t$, and $t$ defined by using $s$, then they’re really merely two different ways of looking at the same thing.

We already know that $t$ is defined in terms of $s$ by construction: $t = f \circ s$. We now want to be able to define $s$ in terms of $t$.

Our first step will be to ensure that, given $t$, we can build a morphism $C \to A$. This is simple enough, we’ve already seen how to do that: require that there exists $g: B \to A$ and rely on composition.

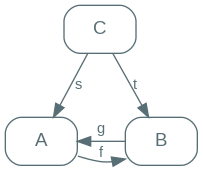
This is almost good enough, but not quite: we don’t want $g \circ t$ to be just any morphism, but to be exactly $s$.

If you follow on the diagram by going $s$, then $f$, then $g$, then it should be pretty clear that what we want is $g \circ f$ to be $1_A$. If seeing it doesn’t convince you, it’s easy enough to reason through it.

We want $s = g \circ f \circ s$. By morphism associativity, this is equivalent to wanting $s = (g \circ f) \circ s$. By morphism unitality, we know that $s = 1_A \circ s$. Bringing these two together, we want $g \circ f = 1_A$.

To summarize, we’ve identified the following constraints for $A$ and $B$ to be the same: there must exist $f: A \to B$ and $g: B \to A$ such that $g \circ f = 1_A$.

We’ve now set things up so that, if $C$ has a morphism to $A$, it will have the same to $B$. We of course also want this to be symmetric, as there’s nothing special about $A$ or $B$ in our argument. And so, by applying the exact same thought process, I hope it’s clear we’ll land on the symmetrical conclusion: we need $f \circ g = 1_B$.

In theory, we would also need to try and enforce two missing constraints: if $A$ has a morphism to $C$, then $B$ must have the same - and vice versa.

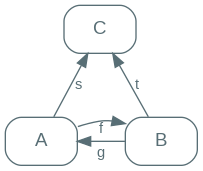
If you just follow through the diagram though, you’ll see that the constraints we’ve set up are already enough: the existence of $s$ not only implies the existence of $t$ (by pre-composition with $g$), but also that $t$ and $s$ are both defined in terms of each other.

So, in conclusion: in category theory, two objects $A$ and $B$ are considered to be the same if there exists both $f: A \to B$ and $g: B \to A$ such that $f \circ g = 1_B$ and $g \circ f = 1_A$.

Two such objects are said to be isomorphic, and $f$ and $g$ are called isomorphisms.